Solving The Rubiks Cube #PID1.2
Solving a Rubik’s Cube isn’t just about memorizing algorithms — it’s about understanding how moves affect the pieces. There are several solving methods, each with its own approach. Some prioritize speed, some focus on efficiency or fewer rotations.
Here’s a breakdown of the main ones:
CFOP: The Classic Speedcubing Approach
CFOP (Cross – First Two Layers – Orientation of Last Layer – Permutation of Last Layer), also known as the Fridrich Method, is the most widely used method among speedcubers. It breaks the solve into four logical steps, enabling high efficiency and minimal pause between sequences.
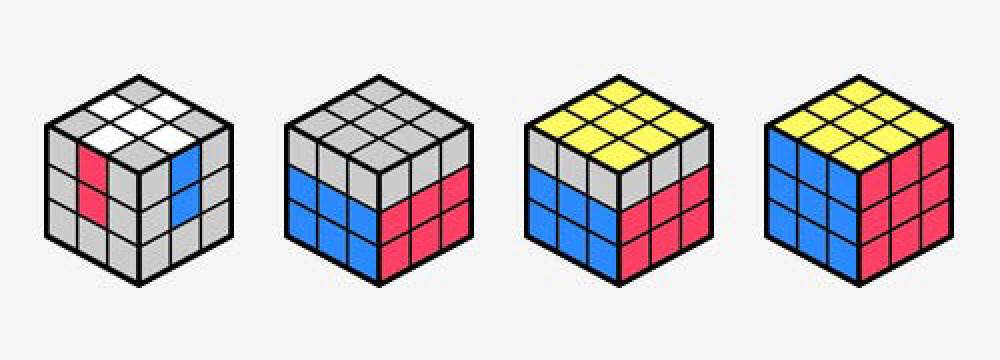
The Cross
The first step is solving a cross on one face of the cube, typically white. The aim is to position the four edge pieces correctly while minimizing moves. Advanced solvers focus on efficiency, ensuring that each edge is inserted optimally without unnecessary cube rotations. Many speedcubers practice solving the cross in eight moves or fewer to optimize their solving time.
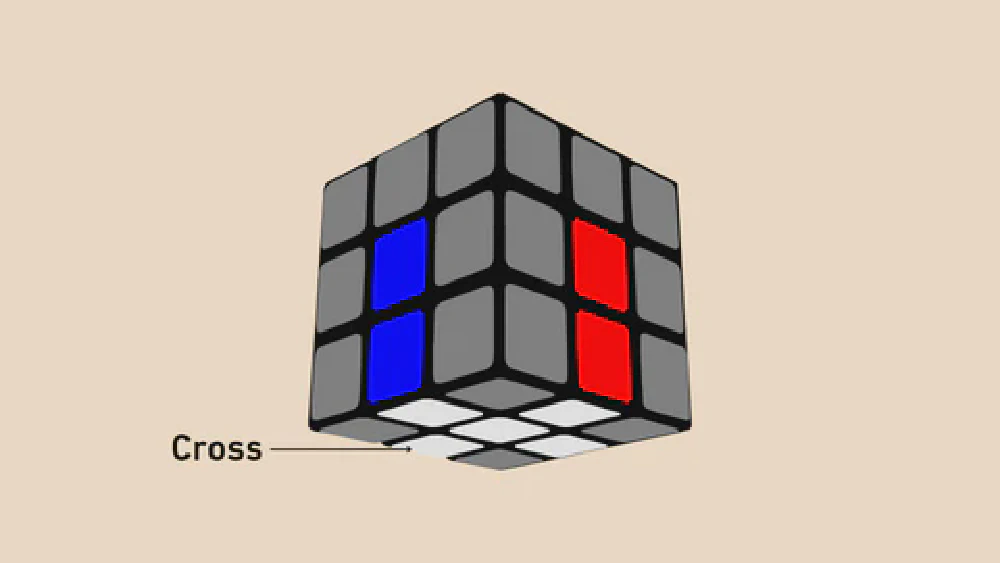
First Two Layers (F2L)
Rather than solving corners and edges separately, F2L pairs them up before inserting them into their respective slots. This is a crucial speed improvement over beginner methods, reducing move count significantly. F2L can be learned intuitively, but advanced cubers memorize key cases and algorithms for increased efficiency.

Orientation of the Last Layer (OLL)
Once the first two layers are completed, the next step is orienting all pieces on the top layer so that the face becomes a uniform color. There are 57 possible cases, but beginners can use a two-step OLL approach with just ten algorithms.

Permutation of the Last Layer (PLL)
The final step is to permute the last layer pieces into their correct positions. This step requires knowledge of 21 algorithms in the full PLL method or just six in the two-look PLL approach. Mastering PLL allows for faster transition times and optimized finger tricks to reduce execution delays.
CFOP is the go-to method for many speedcubers because of its structured approach and ability to handle high turn-per-second (TPS) solves with ease. Even I use CFOP for solving the cube now—I do an intuitive cross and F2L, then use 2-look OLL and 1-look PLL.
For 2x2, I use the CLL (Corners Last Layer) method. You can check out my times here: Cubelelo Profile (it’s unofficial, but yeah!).
Roux: The Efficient Block-Building Method
Roux, developed by Gilles Roux in 2003, takes a vastly different approach from CFOP. It focuses on reducing move count and minimizing cube rotations, making it ideal for one-handed solving. Unlike CFOP, Roux relies heavily on intuitive solving techniques and block-building rather than strict algorithm memorization.
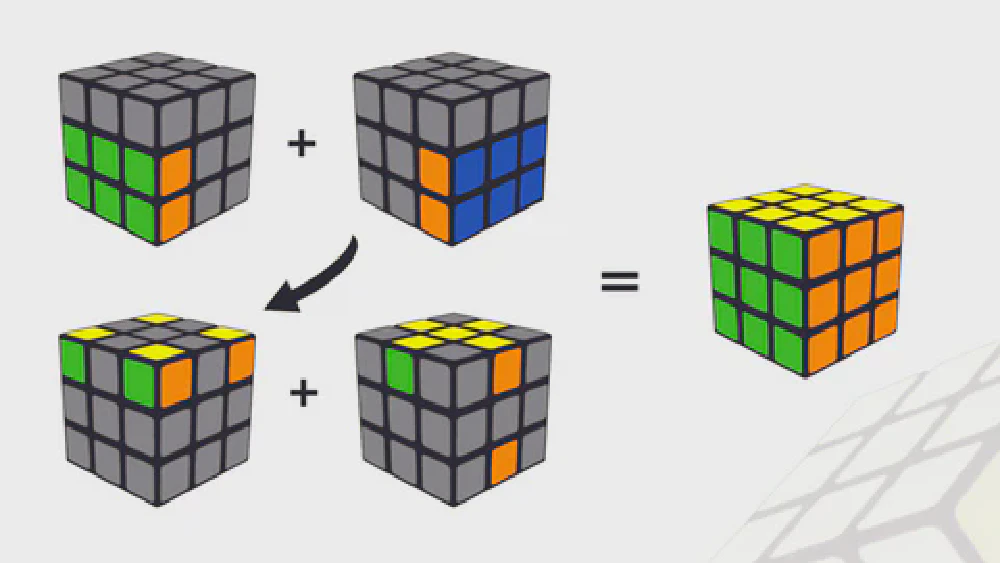
First Block
The solve begins by constructing a 1x2x3 block on one side of the cube. This is done by strategically placing the edge and corner pieces in the correct positions without disrupting already solved parts.
Second Block
A second 1x2x3 block is then built on the opposite side of the cube. At this point, the left and right blocks are complete, leaving only the middle slice and top layer unsolved.
CMLL (Corner Orientation & Permutation)
Instead of solving the last layer in steps like OLL and PLL, Roux addresses all four corners at once using CMLL (Corners of the Last Layer). This step requires only 42 algorithms but can be broken into smaller subsets for easier learning.
LSE (Last Six Edges)
The final stage focuses on solving the remaining six edges using M and U moves exclusively. This step is what makes Roux unique, as it avoids rotations and allows for smooth, fast execution.
The strength of Roux lies in its efficiency—solves often require fewer moves than CFOP, and its reliance on intuitive solving makes it an excellent alternative for those who prefer a different approach.
ZZ: The Method Designed for Ergonomics
The ZZ method, named after its creator Zbigniew Zborowski, aims to balance efficiency and turning ergonomics. It pre-orients edges early in the solve, allowing the rest of the cube to be solved with only R, U, and L moves, eliminating cube rotations and awkward finger placements.
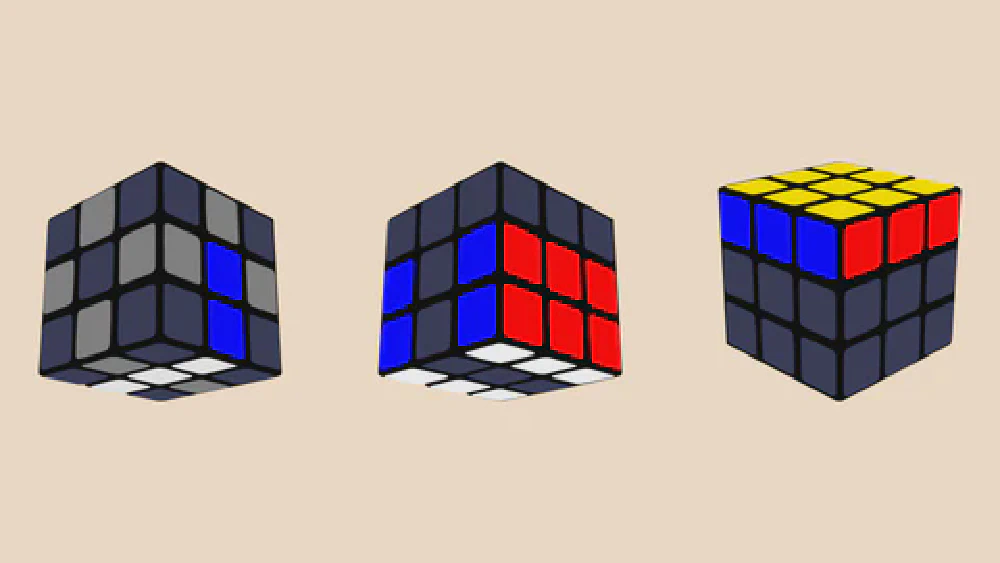
EOLine (Edge Orientation & Line)
The solve begins by orienting all edges while placing two key edges along the bottom. This setup ensures that later steps can be executed smoothly without disrupting edge orientation.
First Two Layers (F2L)
Unlike CFOP, which requires cube rotations for F2L, the ZZ method allows for rotationless F2L execution. Because edge orientation was handled in EOLine, all remaining F2L pairs can be inserted using only R, U, and L moves.
Last Layer
Since all edges are already oriented, solving the last layer can be approached using CFOP-style algorithms or ZZ-specific techniques. The most advanced ZZ solvers use ZBLL (Zborowski-Bruchem Last Layer), which solves the entire last layer in one step, requiring knowledge of over 400 algorithms.
ZZ is an excellent choice for solvers who want to improve ergonomics while maintaining low move counts. However, EOLine can be challenging to master, making it slightly more difficult for beginners compared to CFOP.
Layer-by-Layer (LBL): The Beginner-Friendly Method
The Layer-by-Layer (LBL) method is the most common beginner method. It involves solving the cube in three distinct layers:
- Solve the first layer by completing a cross and inserting corners.
- Solve the second layer by inserting edge pieces into their correct slots.
- Solve the last layer using algorithms to orient and permute the pieces.
This method is easy to learn and provides a solid foundation for more advanced techniques like CFOP.
Petrus Method: The Block-Building Alternative
The Petrus Method, developed by Lars Petrus, is a block-building approach that reduces move count and improves efficiency:
- Solve a 2x2x2 block anywhere on the cube.
- Expand it to a 2x2x3 block.
- Orient the edges early to make solving easier.
- Solve the remaining pieces with minimal moves.
This method is useful for those who want an alternative to CFOP and prefer a more flexible solving approach.
Choosing the Right Method
Each method has its strengths, and the best one depends on your goals:
- CFOP is the best choice for speedcubers aiming for high TPS and efficiency.
- Roux is ideal for solvers who prefer intuitive solving and minimal rotations.
- ZZ is suited for those who want ergonomic solves with fewer rotations.
- LBL is great for beginners starting with the cube.
- Petrus is perfect for those who enjoy a block-building approach.
No matter which method you choose, improving your lookahead, finger tricks, and efficiency will always be key to becoming a faster solver. Try out different approaches and see what works best for you!
Happy cubing!
Related Posts
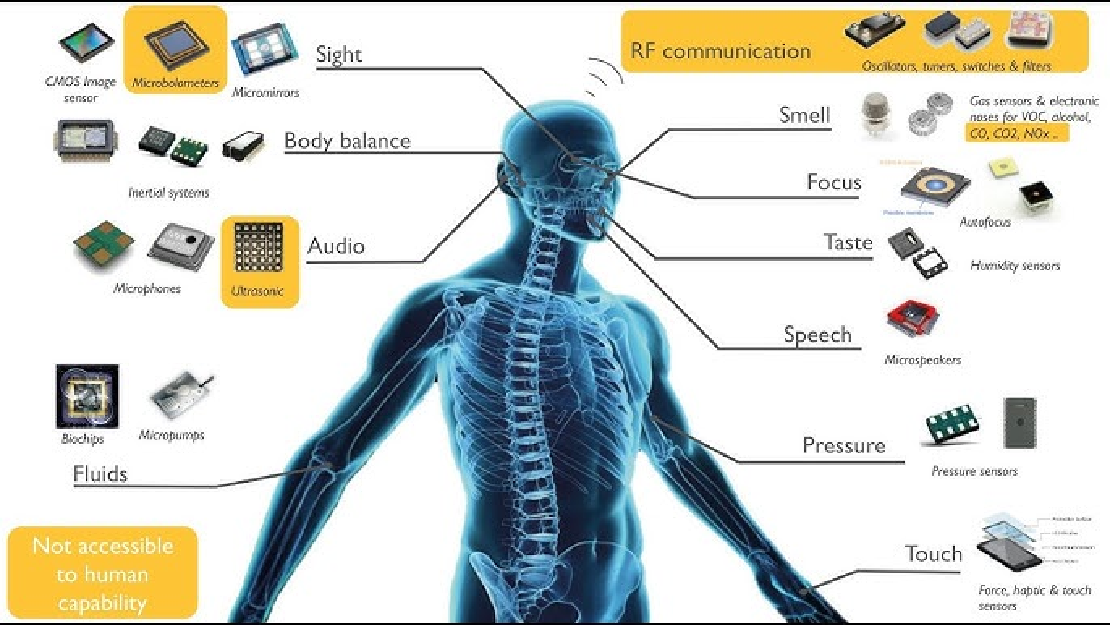
Sensors in Robotics: How Ultrasonic, LiDAR, and IMU Work
Sensors are to robots what eyes, ears, and skin are to humans—but with far fewer limits. While we rely on just five senses, robots can be equipped with many more, sensing distances, movement, vibrations, orientation, light intensity, and even chemical properties. These sensors form the bridge between the digital intelligence of a robot and the physical world it operates in.
Read more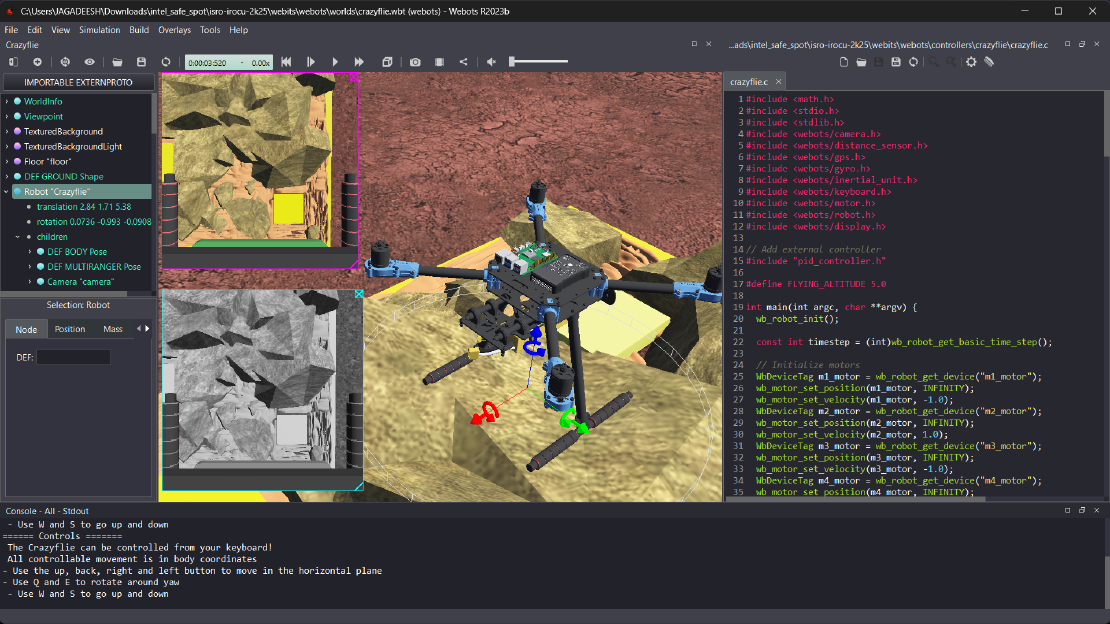
Debugging a Robot In Simulation Before You Burn Wires
Hardware does not come with an undo button. Once you power it on, mistakes—from reversed wiring to faulty code—can result in costly damage. Motors may overheat, printed circuit boards (PCBs) can be fried, and sensors may break. These issues turn exciting projects into frustrating repair sessions. The autonomous drone shown above, designed for GNSS-denied environments in webots as part of the ISRO Robotics Challenge, is a perfect example—where careful planning, testing, and hardware safety were critical at every step
Read more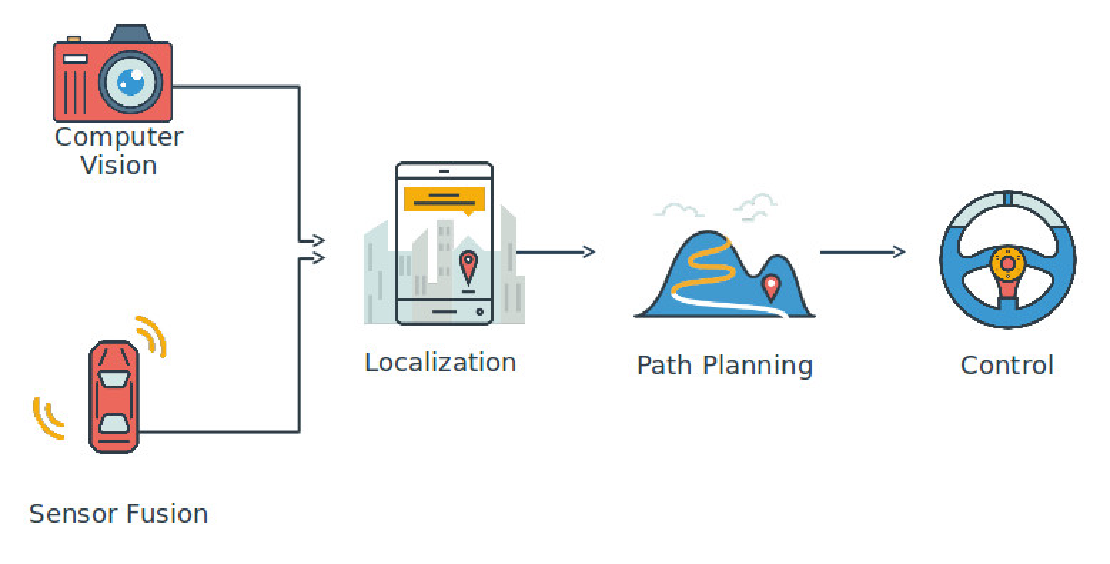
Computer Vision vs. Sensor Fusion: Who Wins the Self-Driving Car Race?
Tesla’s bold claim that “humans drive with eyes and a brain, so our cars will too” sparked one of the most polarizing debates in autonomous vehicle (AV) technology: Can vision-only systems truly compete with—or even outperform—multi-sensor fusion architectures?
Read more