Fixed-Point Conversion Report for EMNIST Neural Network
Introduction
This report describes how I transitioned the EMNIST neural network implementation from floating-point arithmetic to fixed-point representation. The goal was to reduce hardware complexity and improve synthesis compatibility by replacing floating-point computations with fixed-point ones, while preserving accuracy.
Input Vector Representation
The input to the network is a grayscale image of size 28×28 pixels, flattened into a vector of 784 values. Each pixel is originally an 8-bit integer in the range 0–255. To normalize, each pixel is divided by 255, resulting in floating-point values between 0 and 1.
Originally, the normalized input vector was stored as 32-bit floating-point values. In my fixed-point implementation, I represent these normalized pixels as signed 32-bit fixed-point values in Q16.16 format, i.e., 16 bits for the integer part and 16 bits for the fractional part.
Formally, the conversion is:
$$ \mathrm{input_{fixed}} = \left\lfloor \frac{\mathrm{pixel} \times 2^{16}}{255} \right\rfloor $$
where $$2^{16}$$ scales the fractional part.
Weight and Bias Scaling
The weights and biases were analyzed from the W*_memory and b*_memory files to determine their numerical ranges. By inspecting these values, I concluded that 16-bit signed integers are sufficient to store them after appropriate scaling.
To convert floating-point weights and biases to integers, I scaled all values by 10,000:
$$ w_\text{fixed} = \text{round}(w_\text{float} \times 10,000) $$
For example,
$$ 0.1234 \rightarrow 1234 $$
This scaling preserves precision while enabling integer arithmetic internally.
Intermediate Value Range Analysis and Bit-Width Estimation
Using simulation on sample images, I observed the minimum and maximum values of intermediate outputs in each layer as follows:
| Layer | Minimum Value | Maximum Value |
|---|---|---|
| Hidden Layer 1 | 0 | 108,763.886139 |
| Hidden Layer 2 | 0 | 2,829,852,679.626373 |
| Output Layer | -58,500,687,594,725.3047 | 32,406,642,115,926.8281 |
The minimum value is 0 because ReLU truncates negative values to 0
I then calculated the number of bits required to represent these maximum magnitudes, including sign bit:
- For Hidden Layer 1:
$$ \lceil \log_2(108,763.886139) \rceil = 17 \text{ bits} $$
- For Hidden Layer 2:
$$ \lceil \log_2(2,829,852,679.626373) \rceil = 32 \text{ bits} $$
- For Output Layer (taking the largest absolute value from min/max):
$$ \lceil \log_2(58,500,687,594,725.3047) \rceil = 46 \text{ bits} $$
Fixed-Point Format Selection
To maintain approximately 4 decimal digits of precision, I assigned 14 fractional bits for all layers. Therefore, the fixed-point formats I selected are:
| Layer | Format | Integer Bits | Fractional Bits | Total Bits | Comments |
|---|---|---|---|---|---|
| Hidden Layer 1 | Q17.14 | 17 | 14 | 31 | Fits into 32-bit signed integer |
| Hidden Layer 2 | Q32.14 | 32 | 14 | 46 | Requires 64-bit signed integer |
| Output Layer | Q46.14 | 46 | 14 | 60 | Requires 64-bit signed integer |
Implementation Summary
- Input vector: Stored in Q16.16 format as 32-bit signed integers.
- Weights and biases: Scaled by 10,000 and stored as 16-bit signed integers.
- Layer outputs: Use 64-bit signed integers for higher layers to avoid overflow.
- Softmax: Calculated in floating-point (
real) only during simulation; all other RTL code is fixed-point for synthesis.
Accuracy Comparison Between Floating-Point and Fixed-Point
To evaluate the impact of fixed-point conversion on model accuracy, I tested the EMNIST ByClass network (62 classes) across various sample sizes. The model used in this evaluation achieved 91.23% training accuracy and 70.50% validation accuracy, indicating a slightly underfitting scenario. Nevertheless, this level of performance is reasonable for continued testing and prototyping.
It’s important to note that handwriting exhibits high variability. Upon manual inspection, many misclassifications were found to involve case-insensitive characters—such as “o”, “c”, and “s”—which often appear visually similar in both uppercase and lowercase. These inherent ambiguities challenge the model’s ability to distinguish between certain classes, irrespective of numerical precision.
| Sample Size | Floating-Point (IEEE 754) | Fixed-Point (64-bit) |
|---|---|---|
| 10 samples | 9 correct (90% accuracy) | 8 correct (80% accuracy) |
| 100 samples | 76 correct (76% accuracy) | 64 correct (64% accuracy) |
| 1000 samples | 737 correct (73.7% accuracy) | 658 correct (65.8% accuracy) |
| Fixed Point (binary64) | X = 10 | X = 100 | X = 1000 |
|---|---|---|---|
| Confusion Matrix | 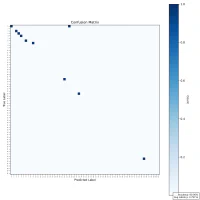
| 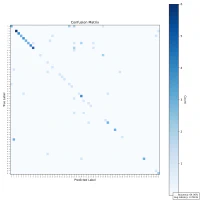 | 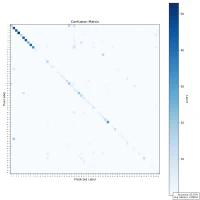 |
| Floating Point (ieee754) | X = 10 | X = 100 | X = 1000 |
|---|---|---|---|
| Confusion Matrix | 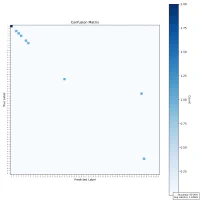 | 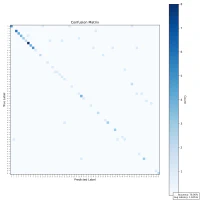 | 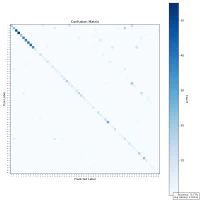 |
While there is a general trend of reduced accuracy with fixed-point arithmetic—particularly as sample size increases—the decline is not strictly monotonic. For example, accuracy rises from 64% at 100 samples to 65.8% at 1000 samples, which contradicts the expected downward trend. This indicates that other factors—such as data distribution, character ambiguity, or rounding effects—may influence the results.
Overall, the reduced precision in fixed-point representation makes it harder to differentiate between visually similar characters, contributing to the observed drop in accuracy. Nonetheless, the results remain promising enough to justify continued testing and prototyping under hardware constraints.
Softmax Implementation in Floating-Point vs Fixed-Point Arithmetic
This report details the comparative analysis and implementation of the Softmax function in two different numerical representations: floating-point and fixed-point arithmetic, both implemented in Verilog HDL. The transition from floating-point to fixed-point was motivated by the need to create a fully synthesizable and resource-efficient pipeline suitable for FPGA-based deployment.
Floating-Point Implementation
Method
Initially, I implemented the Softmax function using Verilog’s real datatype. The exponential function was approximated using a truncated Taylor series expansion, with clamping to avoid numerical overflow. This approach is straightforward and aligns closely with software models.
Code
function real exp_approx;
input real x;
begin
if (x < -10) exp_approx = 0;
else if (x > 10) exp_approx = 22026.46; // Approximate e^10
else exp_approx = 1 + x
+ (x * x) / 2
+ (x * x * x) / 6
+ (x * x * x * x) / 24
+ (x * x * x * x * x) / 120;
end
endfunction
SOFTMAX: begin
exp_sum = 0;
for (i = 0; i < 62; i = i + 1) begin
softmax_output[i] = softmax_act.exp_approx(output_layer[i] - max_output);
exp_sum = exp_sum + softmax_output[i];
end
for (i = 0; i < 62; i = i + 1) begin
softmax_output[i] = softmax_output[i] / exp_sum;
end
state <= DONE;
end
Observations
- Precision: High accuracy and dynamic range.
- Ease of development: Easy to implement and debug due to similarity with high-level numerical computation environments (e.g., Python, MATLAB).
- Limitation: The
realdatatype in Verilog is not synthesizable. As a result, this method is suitable only for simulation or conceptual validation, not for hardware deployment.
Fixed-Point Implementation (Q32.32)
Motivation and Transition
To prepare the model for deployment on FPGAs, I transitioned from the floating-point model to a fixed-point implementation. This allowed me to preserve determinism and synthesizability, while maintaining acceptable numerical accuracy.
The Q32.32 format was selected after empirical testing to balance range and precision. Fixed-point exponentiation was implemented using the same Taylor series method, adapted to integer arithmetic with manual scaling.
Code
function signed [63:0] exp_approx_fixed;
input signed [63:0] x;
reg signed [63:0] x1, x2, x3, x4, x5;
reg signed [63:0] result;
begin
x1 = x;
x2 = fixed_mul(x, x);
x3 = fixed_mul(x2, x);
x4 = fixed_mul(x3, x);
x5 = fixed_mul(x4, x);
result = FIXED_ONE
+ x1
+ (x2 >>> 1) // x² / 2
+ (x3 / 6) // x³ / 6
+ (x4 / 24) // x⁴ / 24
+ (x5 / 120); // x⁵ / 120
exp_approx_fixed = result;
end
endfunction
Supporting arithmetic functions:
function signed [63:0] fixed_mul;
input signed [63:0] a;
input signed [63:0] b;
reg signed [127:0] temp;
begin
temp = a * b;
fixed_mul = temp >>> 32; // Keep result in Q32.32
end
endfunction
function signed [63:0] fixed_div;
input signed [63:0] numerator;
input signed [63:0] denominator;
reg signed [127:0] temp;
begin
temp = numerator <<< 32; // Scale numerator
fixed_div = temp / denominator;
end
endfunction
Softmax Computation in Fixed-Point
SOFTMAX: begin
exp_sum_128 = 0;
// Calculate exponentials in fixed-point Q32.32 using approximation
for (i = 0; i < 62; i = i + 1) begin
// x = output_layer[i] - max_output (Q32.32)
exp_val = exp_approx_fixed(output_layer[i] - max_output);
softmax_fixed[i] = exp_val;
exp_sum_128 = exp_sum_128 + exp_val;
end
// Normalize softmax: softmax[i] = exp_val[i] / exp_sum
// Division approximation: softmax_fixed[i] = (exp_val << 32) / exp_sum
for (i = 0; i < 62; i = i + 1) begin
softmax_fixed[i] = fixed_div(softmax_fixed[i], exp_sum_128[63:0]);
end
state <= DONE;
end
Observations
- Precision: Moderate; sufficient for classification with >65% accuracy on EMNIST using a 64-bit fixed-point implementation.
- Hardware Compatibility: Fully synthesizable and compatible with FPGA deployment.
- Resource Efficiency: Requires more manual tuning and wider data paths (64+ bits) to avoid overflow, but offers deterministic timing and reduced reliance on external IP cores.
Comparison
| Feature | Floating-Point (real) | Fixed-Point (Q32.32) |
|---|---|---|
| Synthesizable | No | Yes |
| Precision | High | Moderate |
| Latency | Variable (simulation only) | Deterministic |
| Resource Efficiency | Low | High |
| Development Complexity | Low | Moderate to High |
| Overflow/Underflow Control | Handled by simulator | Must be manually handled |
| Use Case | Simulation, prototyping | Hardware implementation |
The floating-point implementation served as a proof-of-concept and helped validate the correctness of the neural network logic. However, it was not suitable for synthesis. Therefore, I converted the softmax logic to fixed-point arithmetic to ensure compatibility with hardware constraints.
The fixed-point method, although more complex to implement and debug, provided a fully synthesizable pipeline with acceptable accuracy for embedded vision applications. Careful selection of the Q-format and range analysis was necessary to balance precision and hardware resource utilization.
